Propriétés d’un triangle remarquable
Les anciens avaient découvert ce triangle très spécial, et en utilisaient la plus remarquable propriété pour la construction de leurs bâtiments.
La définition d’un triangle rectangle est simple : l’un des angles est un angle droit. Il est nommé « rectangle » parce que c’est un demi-rectangle, coupé le long d’une diagonale.
Les triangles rectangles obéissent au théorème de Pythagore : la somme des carrés des petits côtés est égale au carré de l’hypothénuse, l’hypothénuse étant le côté opposé à l’angle droit, et qui est également le plus long des trois côtés du triangle.
En général, si les longueurs petits côtés sont des nombres entiers, l’hypothénuse est une racine carrée irréductible. Sauf dans certains cas.
Soit un triangle particulier : une triangle rectangle dont un côté est égal à 3, l’autre à 4, comme dans la figure ci-dessous :
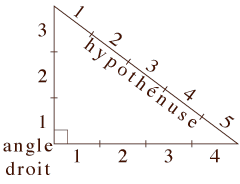
Calculons l’hypothénuse :
3 x 3 = 9
4 x 4 = 16
9 + 16 = 25,
et la racine de 25 est 5.
Donc, en vertu du Théorème de Pythagore, ce triangle est un triangle rectangle.
Pour résumer, nous avons un triangle rectangle dont les trois côtés sont de longueurs respectives 3, 4 et 5. Dans l’absolu, il y a peu de chances pour qu’un triangle ait des côtes qui soient tous des nombres entiers. Et, de plus, ces trois nombres sont assez petits, pas la peine d’aller chercher cette propriété parmi les très grands nombres.
Maintenant, comment utiliser ce triangle simple ? Imaginons un chantier à l’ancienne, un grand chantier, une cathédrale par exemple. Les constructeurs ont aplani le terrain, et il faut tracer le plan sur le sol, en grandeur réelle. Et la construction est basée sur l’angle droit : le transept qui traverse la nef à angle droit, et tous les murs qui se rejoignent à angle droit… Ou bien même une pyramide, dont la base est carrée…
Comment dessiner un angle droit à grande échelle ?
Le moyen le plus simple est bien sûr d’utiliser une équerre. Mais certainement pas une équerre de taille « écolier ».
Il suffit de savoir qu’une erreur d’un degré (à peine perceptible au niveau de l’équerre) donne un écart de 17 cm sur une distance de 10 m, et que pour un bâtiment d’une soixantaine de mètres, l’écart est de plus d’un mètre… Ce n’est pas acceptable ! La cathédrale s’effondrerait !
Le triangle 3-4-5, par contre, nous donne la possibilité de construire une équerre de grandes dimensions, une équerre très facilement transportable, parce que démontable : il s’agit d’une corde à noeuds.
C’est ce que l’on utilisait autrefois sous les nom de « corde à 13 noeuds ». C’était une très longue corde, avec 13 noeuds équidistants, et donc 12 intervalles égaux entre les noeuds. Un constructeur tenait les deux extrémités, un autre tenait le quatrième (3 intervalles entre le 1er et le 2e constructeur), un troisième le 8e (4 intervalles entre le 2e et le 3e, et donc, si on calcule bien, il reste 5 intervalles entre le 2e et le 1er). Une fois que les constructeurs se sont placés de manière à ce que les 3 longueurs de cordes soient bien tendues, on a tracé le triangle 3-4-5 en grande dimension, et donc, au niveau du deuxième constructeur, l’angle est droit.
Ce n’est pas le seul triangle rectangle dont les trois côtés sont entiers. Il y en a beaucoup d’autres. Déjà, avec les triangles 6-8-10, 9-12-15, etc…
Outre les triangles 6-8-10 ou 9-12-15 (qui sont des multiples du triangle étudié), il y a les triangles 5-12-13, 28-45-53, 33-56-65…
